──ポッカリ空いた大きな穴についての考察──
![]()
[Part 4]
________________________________________
■追跡の曲線
〝追跡の曲線〟と〝ベルトラミーの擬球〟のことは、のちになって「改訂増補 ロバチェフスキー空間を旋りて」でも改めて言及されていますので、特にタルホの興味を引いた問題だったことは間違いありません。
先に〝追跡の曲線〟が取り上げられているのは、ロバチェフスキー/ボリアイ幾何学の立体的モデルである〝ベルトラミーの擬球〟を導き出すための前提となるからです。
「宇宙論入門」における〝追跡の曲線〟の記述は、次のようになっています。
或る長さのクサリ乃至糸の両端をとめて、重力場でたらせると、「懸垂線」(Catenary)という曲線ができる。糸は伸びないものとする。そして懸垂線はうごかないものとする。そしてこの糸へ別な糸を捲きつけておいて、Aの所からゆるめないで、引ッぱりながら、ほどいてゆくと、その糸の端はApという別な曲線を描く。これを「追跡線」(Tractrix)と呼ぶ。それは、oからxに向って突走る者を、Aから同一速度で追っかけるときに生じる曲線だからである。このとき直線oxは「漸近線」(Asymptote)となって、無窮遠点で追跡の曲線を切るまで、Apに限りなく近づいてゆく。(「宇宙論入門」、全集5、p.378)
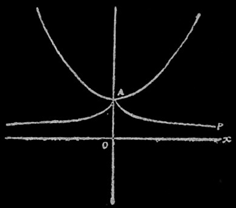
ここでは、〝懸垂線〟〝追跡線〟〝漸近線〟という3つの言葉について説明しています。ただし、〝追跡の曲線〟を〝追跡線〟としています。
この〝追跡の曲線〟は、梶島二郎の『非ゆうくりっど幾何学』にも出てきます。おそらくタルホも参照したであろうこの部分を、梶島本はどのように説明しているでしょうか。
追跡の曲線は、重力の作用する場所で、各部一様で、決して延びない糸の両端を固定したとき表われる懸垂線(Catenary)AQに関係のある曲線である。懸垂線の方程式は、曲線上の一点の座標をx, yとすれば
y=kcosh x/k
で表わされる。
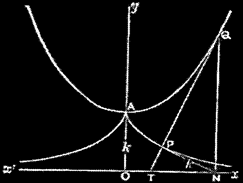
茲に、kは図に示すが如く、懸垂線の最下点Aより軸Oxに下した垂線の長さである。
懸垂線の特質は、其上の一点Qに於ける曲線の切線QTに、Q点の縦線QNの足Nから引いた垂線NPの長さが、Qが曲線上の何れの点で在ても、常に一定でkに等しく、又QPの長さが弧QAの長さに等しいことである。故に懸垂線に沿うて糸を捲き付けて置いて、A点の所から次第にほどけば、糸の端は追跡の曲線APを画く。此場合Oxは漸近線である。(『非ゆうくりっど幾何学』、p.191~192)
両者を比較すると、「宇宙論入門」は梶島本の図にある〝懸垂線〟上のQ点を捨象して、〝追跡線〟の説明をしていることが分かります。そのため、「宇宙論入門」の図は、やや不正確なものになっています。梶島本の説明にあるように、〝QPの長さが弧QAの長さに等しい〟からこそ、〝懸垂線に沿うて糸を捲き付けて置いて、A点の所から次第にほどけば、糸の端は追跡の曲線APを画く〟わけで、その前提を省いた「宇宙論入門」の説明は、かえって分かりにくいものになっています。
この〝懸垂線に沿うて糸を捲き付けて置いて、A点の所から次第にほどけば、糸の端は追跡の曲線APを画く〟という説明の仕方が分かりにくい場合は、wikiの〝トラクトリックス〟の項目のページ(https://ja.wikipedia.org/wiki/トラクトリックス)に、動画を用いて示した図があるので、それを見ると理解しやすいでしょう。
梶島本は、APをなぜ〝追跡の曲線〟というのかという理由を、注によって補足しています。
曲線APを追跡の軌跡というのは、AとOとに動点が在て、Oに在る動点が一定の速さで以てOxの方向に進み、Aに在るものはそれを目標として、絶えず一定の速さを以て追い掛けるとき、後者の軌跡が曲線APとなるからである
上の場合に示した曲線は、二つの動点が同じ速さで進行する場合である(荒川乙吉、数学要義、369頁参照)。(同上、p.193)
■ベルトラミーの〝擬球〟
「宇宙論入門」は、上の〝追跡線〟に引き続き、ベルトラミーの〝擬球〟について説明します。
──さて、Apと同様な曲線は反対側にも得られるから、この両者をいっしょにして、直線oxの周囲に廻転させると、ちょうど蓄音器のラッパを二つ向い合せにしたような表面が出来上る。この奇妙な形を「擬球」(Pseudosphere)と称する。ベルトラミーが考えた双曲線的空間の模型である。(「宇宙論入門」、全集5、p.378)
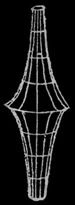
梶島本は、
此曲線AP(y軸に対してAPと対称の位置にある曲線も含めて)を、漸近線xox´の周りに廻転して生ずる表面がベルトラミーが見出した擬球面である。(『非ゆうくりっど幾何学』、p.193)
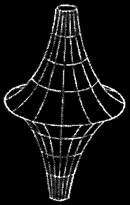
左右に対称的な形ができる〝追跡線〟を、x軸を中心に回転させ、その向きを縦にすると図のような表面を持った立体ができるわけです。タルホが言うように、この〝双曲線的空間の模型〟を考え出したのが、イタリアの数学者ベルトラミー(Eugenio Beltrami, 1835-1900)だったのです。
それにしても、この奇妙な立体は何を意味しているのでしょうか?
「宇宙論入門」はさらに続けます。
ただし、ロバチェフスキー世界の特徴はたての直線によって示されている。これらはたがいに平行していて、無窮遠点に至って合致する。よこの直線は見るごとく世界を一周しているから、リーマン式空間にぞくするものである。このように、モデルは完全だとは云えない。けれども、その初め、幾何学者の勝手な想像だと云われた双曲線的空間は、ユークリッド空間を台とした模型によって表現されることになった。(「宇宙論入門」、全集5、p.378~379)
梶島本は、
併し、図の如き擬球面は双曲線的平面の全部を表わすものではない。それは、無窮遠点に応ずるものは図の上下の二方向に在るのみで、左右は有限であるからである。図の上下の縦の線は、無窮遠点を通る互に平行なる直線に相当し、横の線は限界曲線に相当する。
ベルトラミーの上の研究は、非ユークリッド幾何学とユークリッド幾何学との対立を示したもので、其意味で、此研究は非ユークリッド幾何学の歴史に重大なる功蹟を遺して居る。(『非ゆうくりっど幾何学』、p.194)
梶島本で〝双曲線的平面〟とされているものを、「宇宙論入門」は〝ロバチェフスキー世界〟と言っています。また、梶島本で〝限界曲線〟に相当するものを、「宇宙論入門」は〝リーマン式空間〟としています。
いずれにしても、ベルトラミーの擬球面においては、〝双曲線的平面〟(ロバチェフスキー世界)を表しているのは〝縦方向〟だけである、と言っているのです。無限に引き延ばすことができる〝縦方向〟において、図の縦線が表わす線は、平行線を示しているというわけです。
それに対して、横の線は円を描くので、〝有限である〟と言っています。梶島本の〝限界曲線〟という言葉は、今ではあまり使われないようですが、〝半径無限大の円弧〟のような意味ではないでしょうか。この〝円を描く面〟を、「宇宙論入門」は有限の〝リーマン式空間〟に対比しているわけです。
「宇宙論入門」はさらに続けます。
かたわら楕円空間の方は、すでにユークリッドの球面で代表される。したがって以上両者は、ユークリッド空間における特別な面上の幾何学にあてはまることになり、この両者を元にすれば、ユークリッド幾何学は、ロバチェフスキー幾何学とリーマン幾何学の中間にあって、双方の極限の場合に合致する。故に、非ユークリッド幾何学に矛盾があれば、ユークリッド幾何学に矛盾があることになる。もしユークリッド空間が成立するならば非ユークリッド空間も成立しなければならぬ。かくてこの二種の幾何学の真価は永久に同一である、と云うことになった。(「宇宙論入門」、全集5、p.379)
梶島本は、
それは、数学的に又は論理的にユークリッド幾何学の公理が全部承認されるものならば、論理上、非ユークリッド幾何学は成立しないことになる。然るに、ベルトラミーの研究に依て、双曲線的幾何学は楕円的幾何学と共に、それをユークリッド空間に具体的に表現することが出来るのであるから、若しも非ユークリッド幾何学に矛盾があるならば、それは直にユークリッド幾何学の矛盾となる。是れは、ユークリッド幾何学を認定するならば、不合理のことである。故に、ユークリッド幾何学が成立するならば、同時に非ユークリッド幾何学も成立するもので在て、其結果ユークリッド幾何学の平行線の公理は到底、論理的に証明することは出来ないと云う結論になる。従て、ユークリッド幾何学と非ユークリッド幾何学の数学的、論理的真価は永久に同一であるという断案に導く。(『非ゆうくりっど幾何学』、p.194~195)
上の梶島本は、非常に分かりにくい説明になっていますが、要は、ロバチェフスキー/ボリアイの双曲線的幾何学もリーマンの楕円的幾何学も、ベルトラミーが擬球で示したように、ユークリッド空間に具体的に表現することができるのだから、もし非ユークリッド幾何学に矛盾があるなら、それはユークリッド幾何学の矛盾となり、逆に、ユークリッド幾何学が成立するなら、非ユークリッド幾何学も成立しなければならない、ということを言っているわけです。そこは「宇宙論入門」のほうがより簡潔に要点を述べています。
よって、〝ユークリッド幾何学と非ユークリッド幾何学の真価は永久に同一である〟ということになるわけです。
________________________________________