──ポッカリ空いた大きな穴についての考察──
![]()
[Part 3]
________________________________________
■風変りな曲率を持った空間
さて、ロバチェフスキー/ボリアイやリーマンらによって創始された非ユークリッド幾何学についてタルホは、〝新幾何学の正しい意味を知るには、「宇宙論入門」のペンを執った時まで、待たねばならなかった〟と言っているわけですが、では、その〝新幾何学〟について、「宇宙論入門」ではどのように記述されているでしょうか。これから順を追って見ていくことにします。
「宇宙論入門」には、ロバチェフスキーの名前が最初に次のように出てきます。
ここにきわめて風変りな曲率を持った空間がある。この種の空間はドイツの大数学者ガウスによって初めて発見の端緒がにぎられ、その後、ロシアのニコライ・ロバチェフスキーならびにハンガリーのヨハン・ボリアイによって、ほとんど同時に発見された。(「宇宙論入門」、全集5、p.372~373)
これは「宇宙論入門」第2章の「2─星界幾何学の不可思議」の中に登場します。この冒頭でタルホは、ドイツの数学者ベルンハルト・リーマン(1826-1866)の〝従来の三次元空間は、一般的な三次元幾何学の特別な場合に他ならぬ〟〝三次元幾何学は、任意な次元を持つすべての幾何学についても云える〟(同上、p.371)という言葉を紹介し、その意味するところについて、次のように説明しています。
では、「一般的な立体幾何学」とは何であるか? すでに空間が三次元であるにかかわらず、何をもって特に一般的などと断るのであろう。(中略)一般的な幾何学とは、各種の曲率を持った面或いは立体を取扱うところの幾何学だ、と云うことになる。われわれが学校でならったユークリッド幾何学が、この一般的幾何学の特別な場合、すなわち曲率がゼロなる場合にのみ成立するものであることは、云うまでもなかろう。(同上、p.371)
タルホはここで、〝曲率(Curvature)〟という言葉を持ち出し、それは〝まがりかた〟というほどの意味である、と言っています。そして〝平面幾何学〟と〝球面幾何学〟とを例に挙げ、平面には〝曲率がない(曲率はゼロ)〟といい、〝球面〟や〝玉子の表面〟には〝曲率がある〟という、と説明しています。球面や玉子の表面に曲率があることは誰でも理解できます。しかしながら、〝立体〟が曲率を持つとは一体どういうことか? タルホはいきなり、読者の〝直観力〟を全開にするよう要請します。ただしこの問題については、ここでは立ち入らず、詳しくは後ほど[Part 6]で取り上げることにしましょう。
このように、リーマンの幾何学における曲率の問題を話のまくらにして、次にそれと対照的な性格を持った、〝きわめて風変りな曲率を持った空間〟として、ロバチェフスキーとボリアイの幾何学を紹介しようとしているのです。
そしてリーマンの幾何学では、三角形の内角の和が2直角(180度)より大きいのに対し、ロバチェフスキー/ボリアイの幾何学では、三角形の内角の和は2直角より小さい、と述べています。タルホが言うように、リーマンの幾何学は、球面や玉子の表面など、凸面の形態を思い浮かべれば、そこに描かれた三角形の内角の和が〝2直角より大きくなる〟だろうことは容易に想像がつきます。その反対に、凹面上に三角形を描けば、その内角の和は〝2直角より小さくなる〟ということも想像できるでしょう。
では、ボールを切断したり、玉子の殻を割ったりして、その裏面に三角形を描けば、それがそのままロバチェフスキー/ボリアイの幾何学になるのか? といえば、そう単純な話ではないようです。
〝曲率とはまがりかたと云うほどの意味である〟というタルホの言葉は間違いではありませんが、その前提として、曲率についての数学的な定義を理解しておく必要があるように思います。そうしないと当然、上のような疑問も生じてくるからです。「宇宙論入門」では、曲率の数学的定義を明確にしないまま話が展開されていますが、タルホ自身、曖昧なイメージのまま話を進めているようにも感じられます。
最初のタルホの言葉の中に、〝ガウス〟というドイツの数学者の名前が出てきます。本来ならここで〝ガウスの曲率〟について理解しておくことが必要なのですが、その問題で立ち止まってしまうと、「宇宙論入門」の話の流れを遮ってしまいますので、〝ガウスの曲率〟の問題は、[Part 5]で改めて取り上げることにします。
■3種の幾何学
この後タルホは、曲率の話から、いわゆる〝円錐曲線〟の問題に話題を転じます。楕円(円)、抛物線、双曲線の3つの曲線を例に出し、〝以上、三種のいわゆる「円錐曲線」(Conic Sections)をもって、その後における一般的幾何学の性質が喩えられることになった〟(「宇宙論入門」、全集5、p.373)と述べ、次の3つの幾何学を挙げています。
1. 楕円的幾何学(Elliptic Geometry)
2. 抛物線的幾何学(Parabolic Geometry)
3. 双曲線的幾何学(Hyperbolic Geometry)
この3種の幾何学については、梶島二郎の『非ゆうくりっど幾何学』にも、次のように紹介されています。
現今はクライン(Felix Klein)の命名に基いて、ロバチェフスキー、ボリアイの幾何学を双曲線的幾何学(Hyperbolic Geometry)、リーマンの幾何学を楕円的幾何学(Elliptic Geometry)、ユークリッドのを抛物線的幾何学(Parabolic Geometry)というのが普通である。(『非ゆうくりっど幾何学』、p.25)
このことから、3種の幾何学は、かの〝クラインの壺〟で有名な、ドイツの数学者フェリックス・クライン(1849-1925)の命名であることが判明します。そして、それぞれが次のように対応しているとしています。
1. 楕円的幾何学 → リーマンの幾何学
2. 抛物線的幾何学 → ユークリッドの幾何学
3. 双曲線的幾何学→ ロバチェフスキー/ボリアイの幾何学
さて問題は、その次にタルホが取り上げている〝無窮遠直線〟です。
われわれが取扱っている平面上には、その無限の遠方に「無窮遠直線(Line at Infinity)」と称する直線が横たわっていると仮定して、われわれが現在扱うところのすべての線及び形は、くだんの最遠方に固定された無窮遠直線とのあいだに常に何らかのつながりを持っている。(「宇宙論入門」、全集5、p.374)
タルホはこのように述べて、前記の3つの円錐曲線を以下のように分類しています。
すなわち、
1. 無窮遠直線と交らないものが楕円である。
2. 無窮遠直線と接しているなら、それは抛物線である。
3. 無窮遠直線と交っていたならば、双曲線と云うべきである。
全集版では、無窮遠直線と3種の円錐曲線との関係が図で示されていますが、この図を見ても、読者はさっぱりその意味を理解できないのではないかと思います。

タルホがこの部分を、どんな文献から援用しているのか明らかではありませんが、自身もその意味を理解していたのかどうか怪しい気がします。というのは、これは〝射影幾何学〟の問題で、無窮遠直線と3つの円錐曲線との関係は、その幾何学を俟って初めて理解されるもののようだからです。
たとえば、ネット上にはそれを次のように説明しているものがありますが、
https://www.rikasuki.jp/rika_no95/rika_no95.htm#syaeiheimen
少なくともここで説明されているような内容を理解した上でないと、無窮遠直線と3つの円錐曲線との関係は分からないはずです(ちなみに現在では、〝無窮遠直線〟は〝無限遠直線〟と呼ばれているようです)。
*
次にタルホは、〝エルミット相称〟なるものを持ち出して、〝無窮遠直線〟が〝無窮遠二次曲線〟というものに置き換えられると述べています。これも根拠が示されておらず、このままでは理解のしようがありません。
それを〝図によって示してみよう〟と言ったものが全集版に掲載されていますが、不鮮明なので、それをリライトしたのが以下の図です。
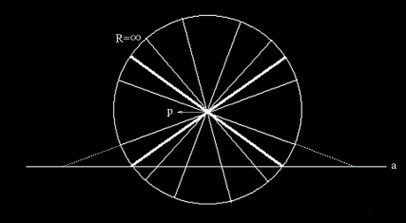
これは先の〝無窮遠直線〟を〝無窮遠二次曲線〟に置き換えた図だと思われますが、〝無窮遠二次曲線〟は〝R=∞〟(半径無限大の円)として示されています。ただし、この図もどんな文献から援用したものか判明しません。
一点pを通って、一直線aに平行な直線が二本引かれることが示されている。なぜなら、平行線とは無窮遠点(無窮遠線上にある点)において交わるものであるからだ。そしてこのpを通る二本の平行線が、aと相交る無数の直線及び相交らない無数の直線とのさかいをなしている。相交らない無数の直線とは、それらが無窮遠二次曲線外で、すなわち「あの世」において交ることの謂である。(同上、p.374)
このように述べており、図中の2本の太い線で示されているのが平行線だと思われます。ちょうど無窮遠線(R=∞の円)上で直線aと交わっているからです。そして〝aと相交る無数の直線〟とは、R=∞の円の内で直線aと交わっている直線を指しており、〝相交らない無数の直線〟とは、R=∞の円の外でaと交わる直線(円の外は点線で表されている)のことを言っているのでしょう。
しかしながら、この図で理解しにくいのは、直線aが、R=∞の円の〝外〟まで延長して描かれていることです。そうすると、〝半径無限大の円より長い直線〟が想定されているわけで、矛盾が生じます。タルホもここで、半径無限大の円の〝外〟を「あの世」と形容していますが、そうすると無限大に〝内〟と〝外〟を想定することになり、これも論理矛盾になります。
ともあれ、タルホは次のように続けます。
ロバチェフスキー及びボリアイの定理にも、次のようにある。
「直線外の一点を通って、これと相交る直線及び相交らない直線はいずれも無数に存在し、且つその点を通ってこれに平行な直線は二本引ける」
ところがリーマンの定理では、
「一直線外の一点を通ってこれと交らぬような直線は存在しない」このためには地球の表面を考えたら十分である。(同上、p.374~375)
つまり、これまで図によって説明してきたのは、3種の幾何学のうち、ロバチェフスキー/ボリアイの幾何学(双曲線的幾何学)についてだったわけです。
そして、一方のリーマンの幾何学(楕円的幾何学)では、〝平行線は1本も存在しない〟ということになり、それを理解するには、たとえば地球の表面を考えてみるとよいと言っているのです。地球儀上に縦に引かれた経度を表す直線(平行線)は、すべて両極(北極・南極)で交わってしまうからです。
*
この後、「宇宙論入門」は、物理学者のヘルムホルツの話に移っていくのですが、ここでは順序を入れ替えて、〝追跡の曲線〟と〝ベルトラミーの擬球〟の話を先に持ってこようと思います。
なぜなら、ロバチェフスキー/ボリアイ幾何学の平行線の問題を、平面的に図示して説明したのがこれまでの話で、ではそれを立体的に表現できるだろうか、というふうにつなげていったほうが、話の展開の仕方として分かりやすいのではないかと考えるからです。
________________________________________